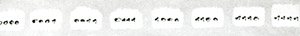Manfred Mohr: Themes / Ideas

Combinatorics in my art work 1963 - 2015

I used combinatorics in many different ways over the years. The artworks below exhibit the various ideas I had.

click on images below for associated webpages and details

Early Combinatorial Ideas 1963, 1966, 1967

I intuitively used combinatorics before I knew the logic of it

Painting showing Combinations of 0 and 1 taken 4 at a time: Bild 116/63 1963
	8 of the 16 combinations of 0 and 1 taken 4 at a time are shown in this painting

4 Paintings used as Combinatorial Elements with Overlapping Visual Information - Bild C-66 1966

The 4 paintings can be arranged in all combinations of 2 x 2 or 4 x 1. The visual imformation overlaps on all 4 sides forming continuous patterns over the borders of the individual paintings.

3 Paintings used as Combinatorial Elements with Non-Overlapping Visual Information - Konkreter Text I, 1967

The 3 paintings can be arranged in all combinations of 1 x 3 paintings. The visual information does not overlap from one painting to another, each part is independant.

Combinatorial Ideas in Cubic Limit I 1973 - 1975
The 12 lines of the cube are used as an alphabet. The drawings and films show combinations of n lines at a time (n = 0 to 12).

Combinatorial elements in my computer generated films "Cubic Limit" and "Complimentary Cubes" 1973 - 1974

Some images from film "Cubic Limit" showing lines n at a time, 1973-1974	Some images from film "Complimentary Cubes" showing 2 cubes, one with n lines, the other its complimentary cube with 12 - n lines, 1973-1974
Sequences from these 2 films are published in the catalog "Manfred Mohr, "Cubic Limit", Galerie Weiller, Paris, 1975"

P-161. A series of 13 drawings showing the combinatorial possibilities of lines of a cube taken n at a time at a given rotation (where n = 0 to 12) 1975

A series of 13 drawings from this algorithm is published in the catalog "Manfred Mohr, "Cubic Limit", Galerie Weiller, Paris, 1975"

Combinatorial Ideas in Dimensions I 1978
The graph of the 4-D hypercube is used in this workphase. The concept of diagonal paths is introduced. Combinatorics are used in many ways in the algorithms associated with this workphase.

P-228 1978
All the possible diagonal paths between 2 diagonally opposite vertices on the graph of the 4-D hypercube for all the possible diagonally opposite vertices.

This is a series of 8 drawings which show the combinatorics in 2 ways:

Each drawing shows all the combinations of diagonal paths between a given pair of diagonally opposite vertices.
Each of the 8 possible pairs of diagonally opposite vertices is shown in one drawing.

A diagonal path is a set of edges along the structure of the hypercube, changing one dimension at a time and visiting each dimension once. The diagonal paths are represented graphically by a connected set of 4 edges and each vertex on the path is represented by its binary value 0 and 1 taken 4 at a time.

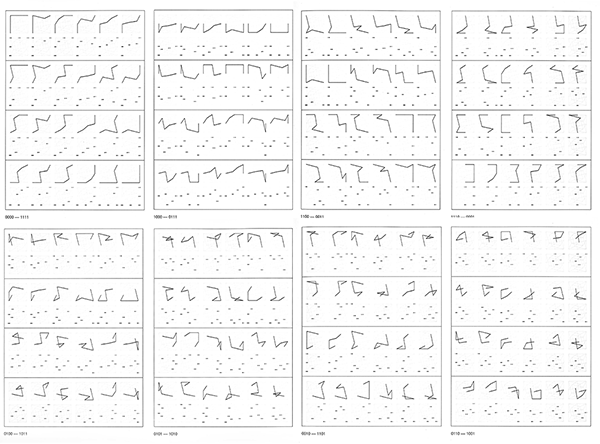
This series of 8 drawings is published in the catalog Manfred Mohr, "Dimensions", Galerie Mueller-Roth, Stuttgart 1979

P-229 1978

Wooden wall structure of 24 pieces showing all the possible diagonal paths between the vertices 0000 - 1111 on the graph of the 4-D hypercube

This wall piece is published in the catalog Manfred Mohr, "Dimensions", Galerie Mueller-Roth, Stuttgart 1979

P-231 1978

All the 112 maximally planar graphs possible between the 2 diagonally opposite vertices 0000 - 1111 on the graph of the 4-D hypercube

These graphs are formed from diagonal paths. Planar graphs are graphs where there are no crossings except along the edges and vertices of the structure of the 4-D hypercube. These graphs are maximal since they contain the maximum number of diagonal paths that fit this criteria.

These drawings are published in the catalog Manfred Mohr, "Dimensions", Galerie Mueller-Roth, Stuttgart 1979

P-226 1978

The 32 edges in the graph of the 4-D hypercube are divided into 4 equal sets of 8 lines each and recombined in a "magic square".

The "magic square" by its nature has a combinatorial element to it. In the case of a 4 x 4 "magic square", 10 of the 24 possibilities are used. In a "magic square", the 4 horizontal rows, the 4 vertical columns, and the 2 diagonals add up to the complete structure.

These drawings are published in the catalog Manfred Mohr, "Dimensions", Galerie Mueller-Roth, Stuttgart 1979

Combinatorial Ideas in Divisibility I, II, III 1980 - 1985 A cube is divided into 4 parts by its horizontal and vertical cartesian planes. The 4 parts have different rotations. This creates a "4-cut" where the "out-lines" form shapes and the "in-lines" form signs. Divisibility I shows the '4-cut", Divisibility II shows the initial "4-cut" as a seed which generates the growth of subsequent "4-cuts". Divisibility III shows the spine of the growth and the forms of each generation.
P-308 1980-1985 All possible 2-D projections of the 3-D "4-Cut". The projections are on the X-Y, X-Z, and Y-Z planes.
P-380 1985 All possible growth patterns after four generations from the same initial "4-cut". 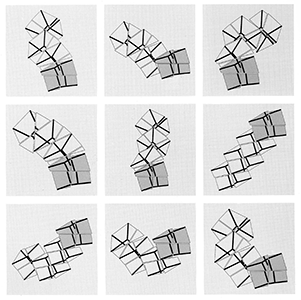This drawing is published in the catalog Manfred Mohr, "Divisibility III", Galerie Mueller-Roth, Stuttgart 1986

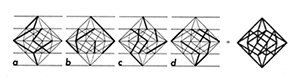
Combinatorial Ideas in Dimensions II 1986 - 1989 This workphase shows 4-D hypercube with rotation. The eight intertwining 3-D cubes which make up the 4-D hypercube are the subject of this work. Each inherent cube is clipped by a square frontal window. Four of the clipped cubes are black and 4 of the clipped cubes are gray.
P-414 1988 All possible combinations of 4 black clipped cubes and 4 gray clipped cubes inherent in the 4-D hypercube at a given rotation. This drawing is published in the catalog "Manfred Mohr, Arbeiten 1960-1988", Reuchlinhaus, Pforzheim, 1988

Combinatorial Ideas in Line Cluster 1989-1990 The 5-D hypercube is used here. Four lines from each dimensional direction are chosen to be displayed. One of the four lines of each dimensional direction is thick, the others are thin.
P-452 1989 All possible 2-D projection of a 5-D hypercube for a given set of lines and a given rotation. 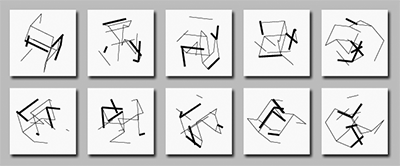This drawing is published in the catalogs "Laszlo Moholy-Nagy / Idee und Wirkung" Kunsthalle Bielefeld, 1995 and "Manfred Mohr, Algorithmische Arbeiten", Josef Albers Museum, Bottrop, 1998

Combinatorial Ideas in Laserglyphs 1990 - 1993
The 6-D hypercube is used here. A 6-D hypercube has 32 diagonally opposite vertices. For each diagonally opposite set of vertices there are 720 diagonal paths along the edges of the structure connecting these vertices.

P-480 1992
Shown here are 2 of the 32 possible drawings each linking diagonally opposite vertices of the 6-D hypercube. Each drawing shows the 720 diagonal paths for the pair of diagonally opposite vertices.

These drawings are published in the monography "Manfred Mohr", Waser Verlag Zurich, 1994

P-499 1993

Laser-cut steel relief of all the 15 possible 2-D projections of a chosen diagonal path through a 6-D hypercube

This 15 part relief is published in the monography "Manfred Mohr", Waser Verlag Zurich, 1994

Combinatorial Ideas in Artificiata II, 2012 - 2015
A diagonal path from a 3-D to 100-D hypercube is generated. Horizontal lines are attached to the path at each change of direction. The areas between 2 adjacent horizontal lines are randomly colored.

Artificiata II, projections, 2012 - 2014

P-1640 2014
All 55 combinations of 2-D projections of a diagonal-path from an 11-D hypercube

Artist book "Articificata II" 2014
All 66 combinations of 2-D projections of a diagonal-path from an 12-D hypercube

P-1632 2014, Wall installation
All 55 combinations of 2-D projections of a diagonal-path from an 11-D hypercube

Artificiata II, projections and dimensions 2014 - 2015
All the combinations of 2-D projections of a diagonal path of a hypercube from 2-D to 13-D are shown

P-1660 2015
a computer-generated real-time algorithmic animation
all the 2-D projections of a randomly chosen n-dimensional diagonal path between 2-D and 13-D in a cyclic sequence are shown

P-1650 2014
Series of 13 drawings showing all the 2-D projections of a diagonal path of a hypercube from 2-D to 13-D

P-1660 2014
A short movie of the real-time animation was shown at Digital Art @ Sony Center Screen 2015
click image for movie